Graph

A graph is a set of vertices (points) connected by edges (lines).

We use specifics graph algorithms to efficiency resolve related problems.

Structure

$$G=(E,V)$$

• $G$: graph
• $V$: vertices. The nodes of the graph.
• $E$: edges. Directed or undirected links between the vertices.

Adjacency matrix

An adjacency matrix helps to quickly look up a single edge and allows for quick addition of edges.

The graph must be (almost) complete and it can cost performance depending on its size.

Performances

$V$ is the number of vertices

• Browse a row or a column of the matrice (adjacent node/edge): $O(V)$
• Store the matrix: $O(V²)$
• Browsing all edges of the graph: $O(V²)$

Adjacency list

An adjacency list provides quick lookup of one vertex and allows for quick addition of new edges and vertices. However, searching for a single edge requires traversing the entire list.

Performances

$V$ is the number of vertices $E$ is the number of edges

• Store the lists: $O(E+V)$
• Browse all vertices of the graph: $O(E+V)$
• Check if $(v_1,v_2)$ is a vertice: $O(\mathrm{deg}(v_i))$
• Browse adjacent vertices of $v_i$ : $O(\mathrm{deg}(v_i))$

Types

Directed vs. undirected

(WIP)

Eulerian vs. Hamiltonian

• Eulerian path: a path that visits each edge of the graph only once
• Hamiltonian path: a path that contains each vertex only once (e.g. Traveling Salesman)

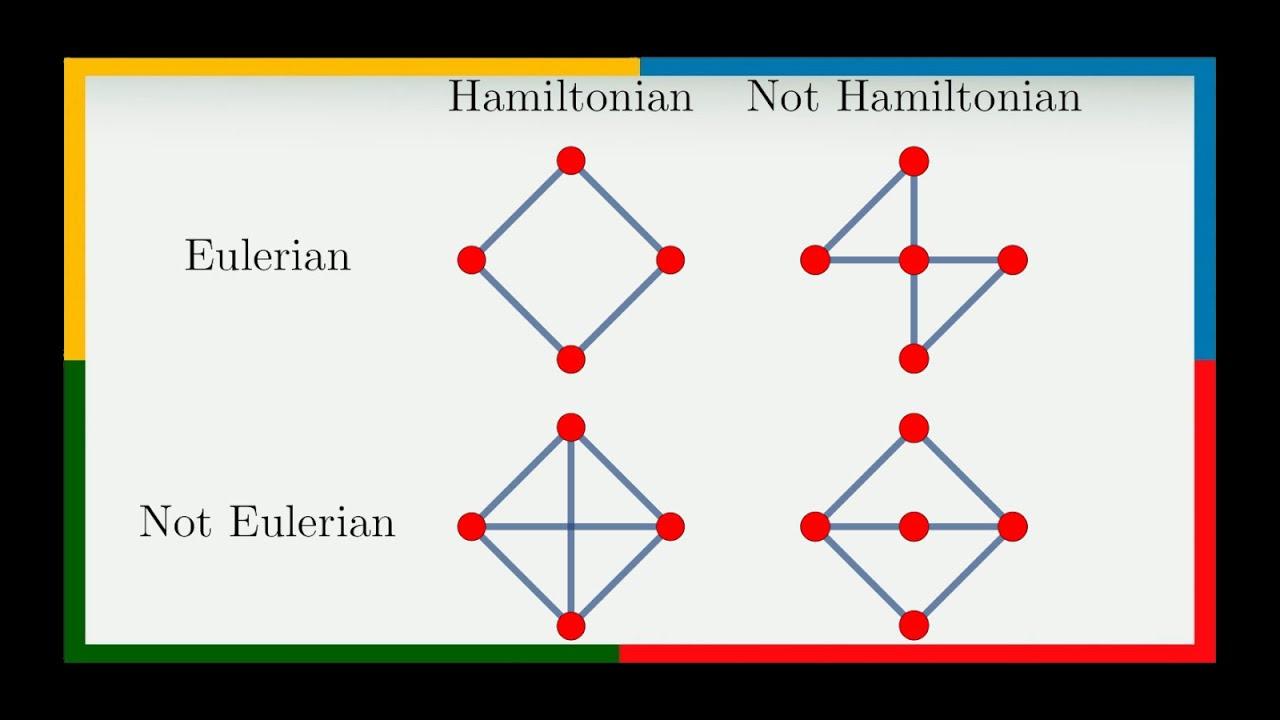Source: VisualMath – Youtube

Bipartite

A graph is bipartite if the vertices can be split into two subsets

Clique

A clique is when you take a subset of vertices and all these vertices are connected together.

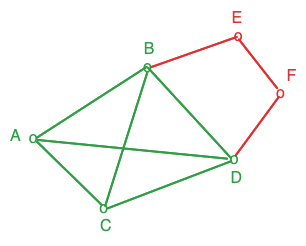
On the left, $(A,B,C,D)$ are a clique because they are all adjacent to each other. It's not the case for $(B,E,F,D)$

Algorithms

• Find if path exists between 2 nodes
  • Directed graphes: Tarjan, Kosaraju
  • Undirected graphes: DFS, BFS
• Find shortest path between 2 nodes
  • Bellman-Ford
  • Dijkstra (positive weights only)
  • Floyd-warshall (positive and negative, find shortest path for all nodes)
• Connect all vertices together with edges subsets (Minimum Spanning Tree)
  • Prim (denses graphs)
  • Kruskal (less denses graphs)