Newton's method

Newton's method is an algorithm to find the real zeros of a function with the derivative of the function to find its roots.

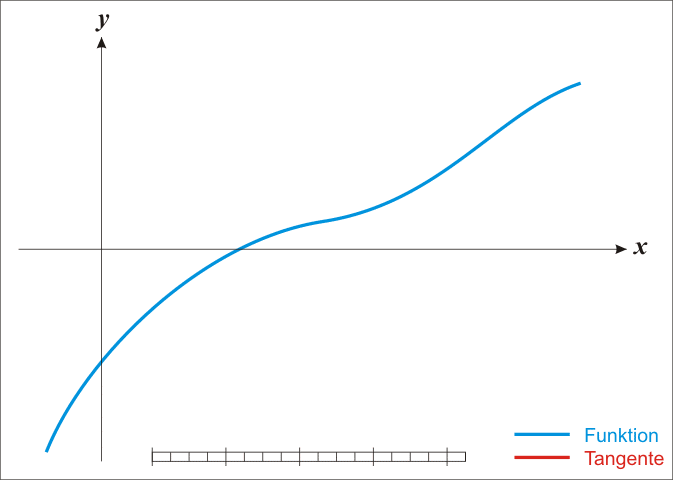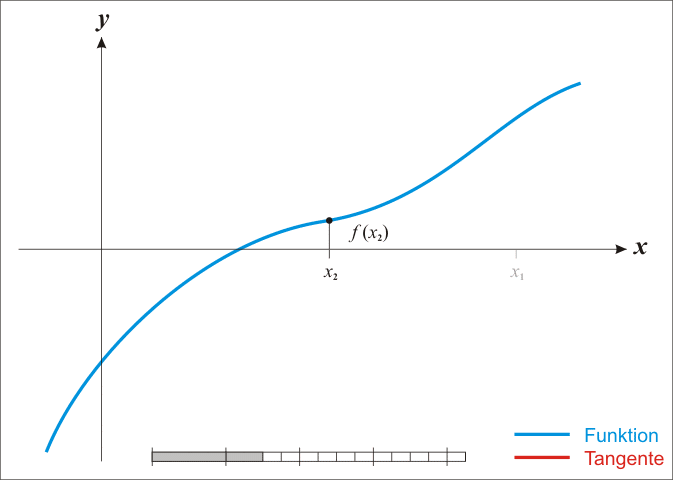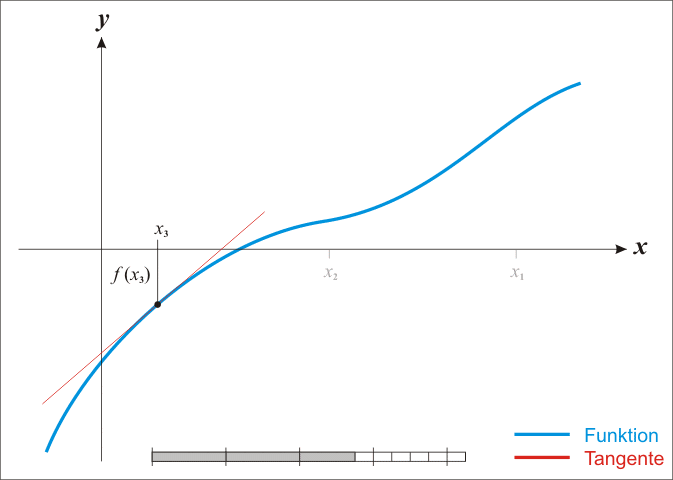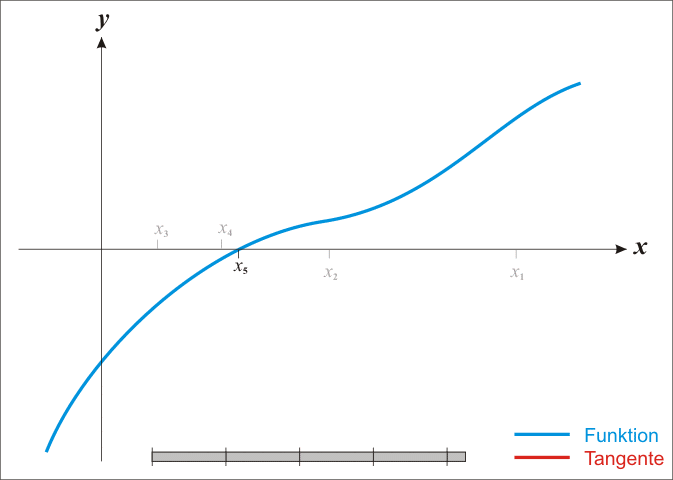
Algorithm

Each new value are found with the following equation:

x_{n + 1} = x_{n} - \frac{f (x_{n})}{f^{'} (x_{n})}

$x_{n}$ is the initial guess, $x_{n + 1}$ is the next guess

The derivative can be approximated by the secant method:

f^{'} (x_{n}) = \frac{f (x_{n}) - f (x_{n} - 1)}{x_{n} - x_{n - 1}}

Newton's method can be used with a multi-variable function. We need for that to use derivative matrix

If $x = 0$ , it's a zero-divison. We need to change our $x_{1}$ value
Sometimes, if the initial guess is too far, and depending of the function, the algorithm may find the answer slowly or not at all.