Time complexity

We define time complexity as the time a computer take to run an algorithm.

The time to run operations grow with the input size, e.g. items in an array or vertices and edge in a graph.

Approaches

Depending on the size of the problem, we have to balance speed over precision. If we have a complex problem with a lot of data, maybe we'll need to find a good solution quickly rather than the perfect solution slowly.

Category	Size	Typical approach
Tiny	Exhaustive	$n\approx 10$
Small	Implicit	$10\le n\le {10}^2$
Standard	Metaheuristic	${10}^2\le n\le {10}^4$
Big	Decomposition	${10}^4\le n\le {10}^7$
Huge	Big data	$n>{10}^7$

Notation

Big O

The Big O notation shows how an algorithm's performance get bigger as its input $n$ increases. In short: how does the time it takes to do the operation growth as we add more elements.

Notation	Name	Example
$O(1)$	constant	Determine if number is even or odd
$O(\log n)$	logarithmic	Binary search
$O(n)$	linear	Find item in an unsorted list/array
$O(n\log n)$	linearithmic	(to complete)
$O(n^2)$	quadratic	(to complete)
$O(n^3)$	cubic	(to complete)
$O(n^c)$	polynomial	(to complete)
$O(2^n)$	exponential	(to complete)
$O(n!)$	factorial	(to complete)

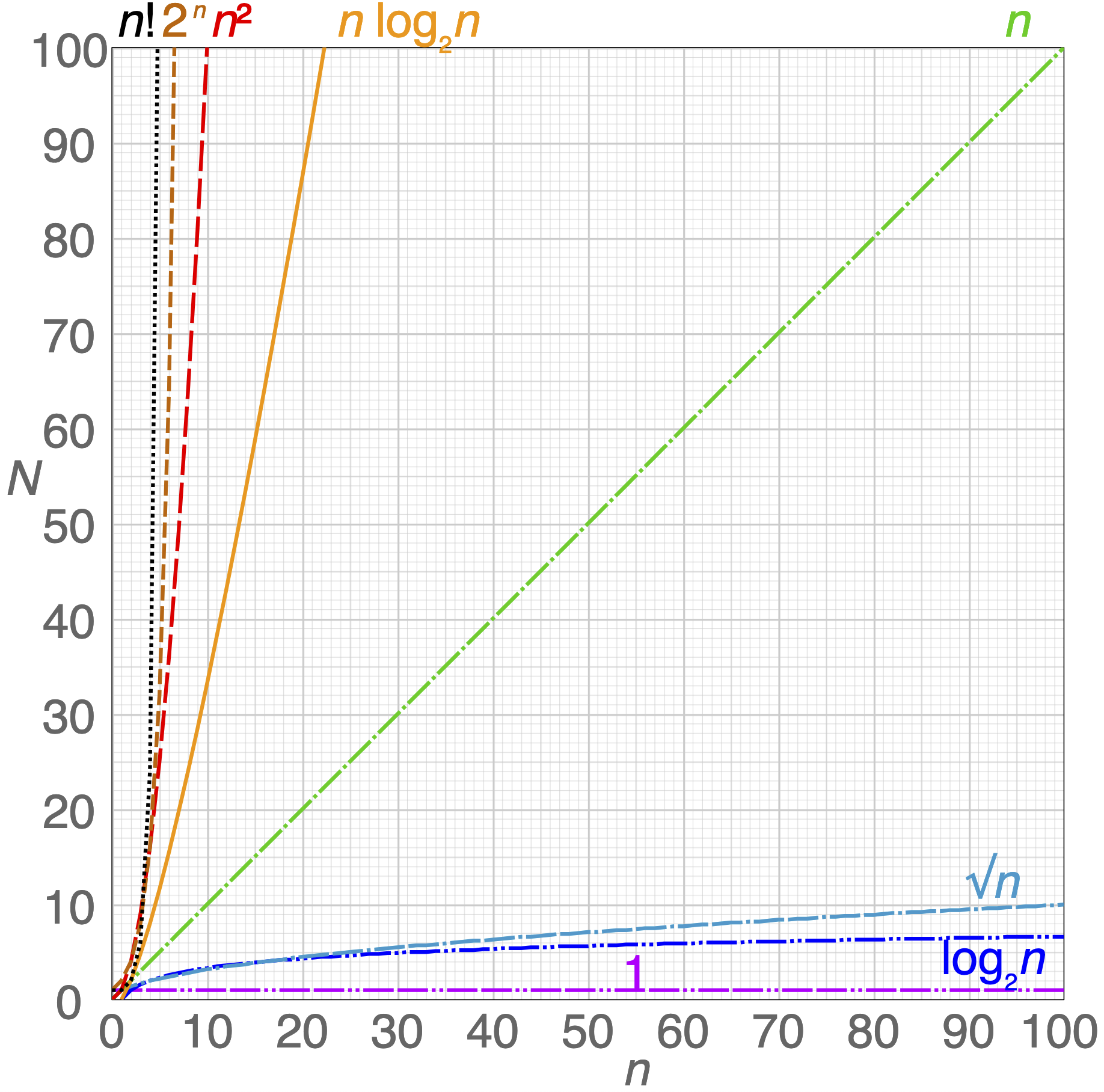
Keep in mind notation can have more than one type of input. Two different lists could involve a $O(n+m)$ type of complexity, or $O(n\times m)$ if they depend on each other. We typically use notation like $O(|V|+|E|)$ in graphs, where the number of vertices and edges can influence the performances.

Example Let say there is 100 persons, you give a coin to one of them, and you have to find it. They can only answer by yes or no.

Scenario	Algorithm	Complexity
Give the coin to someone	You throw the coin in the group without looking	$O(1)$
The person who has the coin is the only one to know	You ask each person individually "do you have the coin?".	$O(n)$
Everybody know where is the coin	You divide the group in half and ask in which sub-group the coin is. You repeat the processus until you find it.	$O(\log n)$
Only one person know on which person the coin is hidden	You take the 1st person and ask for every person if they have the coin. You repeat the processus for every other person.	$O(n^2)$

Big Omega / Theta

As Big O notation define the worst-case scenario for an algorithm, Big Omega and Big Theta define respectively the best and mean case.

Example Back to previous example: there is 100 persons, one of them has coin. You ask to each of them if they have it.

• Best case: you're lucky and find the person on the first time. It took you $\mathrm{\Omega }(1)$ time.
• Worst case: the last person you asked is the one with the coin. It took $O(n/2)$ time.
• Mean case: on average, you need to ask ~50 persons to find the coin, so $\mathrm{\Theta }(n)$ time.

Simplifications

We usually simplify the complexity notation, because it's the growth rate over time that is really interesting.

In the previous example, finding a coin among 100 persons would need to check ~50 persons on average, so $\mathrm{\Theta }(n/2)$. What really matters is that the more persons there is, the more time we'll take to find the coin: this growth in linear. So, we drop constants numbers as it's not vey relevant. The average time complexity is $\mathrm{\Theta }(n)$.

Some examples

Example	Simplification	Explanations
$O(n+n²)$	$O(n²)$	$n^2$ will have more impact over $n$, so we simplify to a quadratic complexity.
$O(n\times n^2)$	$O(n^3)$	As it's a multiplication, we simplify mathematically the term. The growth is the cubic.

Complexity classes

Based on their time complexity, algorithms can be categorised in different complexity classes. You can check the complete list, but here are some of the most common ones.

P

P is a polynomial time solvable problem.

It takes $O(n^c)$ or less to find (or verify) a solution. Since those problem are relatively easy, we can use efficient algorithms to solve them.

Examples

• Sorting algorithms: quicksort, bubble sort, merge sort, etc.
• Shortest path in a graph

NP

NP is a non-polynomial time solvable problem. It takes more than $O(n^c)$ to find a yes/no solution (e.g. is the puzzle complete), but it's verifiable in polynomial time.

For example, you can easily check if a sudoku puzzle is solved by check the row and columns containing the 9 numbers, but it takes more time to complete it.

Algorithms usually rely on approximations (e.g heuristics) to find solutions for these kind of problems.

NOTE

NP stands in fact for Nondeterministic Polynomial. It basically means that it should be solvable in polynomial time with theoretical nondeterministic machines.

Sub-classes

• NP-complete: if we find a polynomial time algorithm to solve these problems, we could solve any other NP problems.
• NP-hard: it's at least as hard as NP-complete problems, but it's also non-polynomial to verify the solution.

Examples

• Finding prime number (NP)
• Traveling Salesman, Knapsack, Graph coloring (NP-complete)
• Halting (NP-hard)

Problems

• P vs. NP

Resources

• bigocheatsheet.io – Cheatsheet containing data structures and algorithms
• bigocheatsheet.com – Overview with chart and tables
• Big O notation in 5 minutes – Youtube